Momentum of Fireworks Their Center of Mass Will Continue on the Same Trajectory
Last time, we derived the principle of conservation of linear momentum. Before we move on, let's do a couple of examples where we put it to work.
Exercise: breaking up
A hockey puck is traveling in the \( +\hat{x} \) direction at constant speed \( v_0 \) m/s. Suddenly, it breaks apart into two pieces which travel off at \(\theta_1 = 60^\circ\) and \(\theta_2 = 30^\circ\) as pictured:
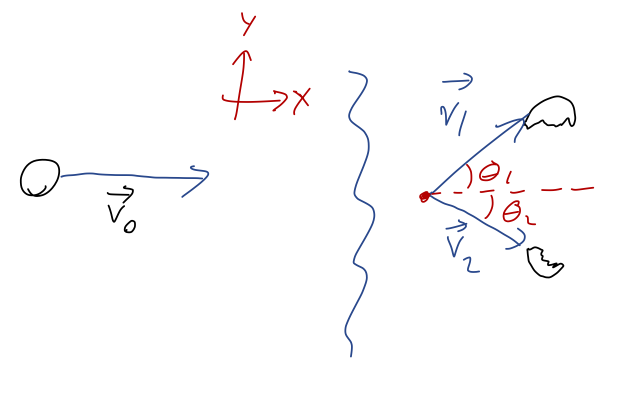
If the first piece is moving at \( v_1 = 4 \) m/s, and its mass is equal to \( 2/3 \) of the total mass of the hockey puck, what is the speed \( v_2 \) of the other piece?
(Once again, this is an exercise - if you're catching up on these notes and haven't looked at this yet, try to solve it before reading on!)
Since there are no external forces, we have conservation of total momentum \( \vec{P} \), which is most usefully written as \(\vec{P}_{\rm initial} = \vec{P}_{\rm final}\). This gives us two conservation equations, one for the \( \hat{x} \) components and one for the \( \hat{y} \) components:
\[ \begin{aligned} (m_1 + m_2) v_0 = m_1 v_1 \cos \theta_1 - m_2 v_2 \cos \theta_2 \\ 0 = m_1 v_1 \sin \theta_1 - m_2 v_2 \sin \theta_2 \end{aligned} \]
To relate \( v_2 \) to \( v_1 \), we can just use the second equation for the vertical components. Doing some algebra,
\[ \begin{aligned} m_1 v_1 \sin \theta_1 = m_2 v_2 \sin \theta_2 \\ v_2 = \frac{m_1 \sin \theta_1}{m_2 \sin \theta_2} v_1 \end{aligned} \]
If the total mass of the hockey puck is \( M \), then since \( m_1 = 2M/3 \), we know that \( m_2 = M/3 \), since they have to add up to \( M \). So \( m_1 / m_2 = 2 \). Plugging in \( \sin \theta_1 = \sqrt{3}/2 \) and \( \sin \theta_2 = 1/2 \), we end up with
\[ \begin{aligned} v_2 = 2 \sqrt{3} v_1 = 8 \sqrt{3}\ {\rm m} / {\rm s}, \end{aligned} \]
or about 13.8 m/s.
We only had to use conservation of momentum in the \( \hat{y} \) direction to get this far, so we still have the other equation involving \( P_x \). We could continue and use that equation to find the only unknown quantity left, which is the speed \( v_0 \). But this won't really be any different from the calculation we just did, so I'll stop here.
Example: momentum conservation
I'm standing on a boat in a completely still lake, near a dock. Everything starts at rest. If I walk at constant speed on the boat, in the direction away from the dock, how does the distance between me and the dock change?
There's a few things to keep track of here: the boat, the dock, and me. Step one is to sketch some coordinates, then:
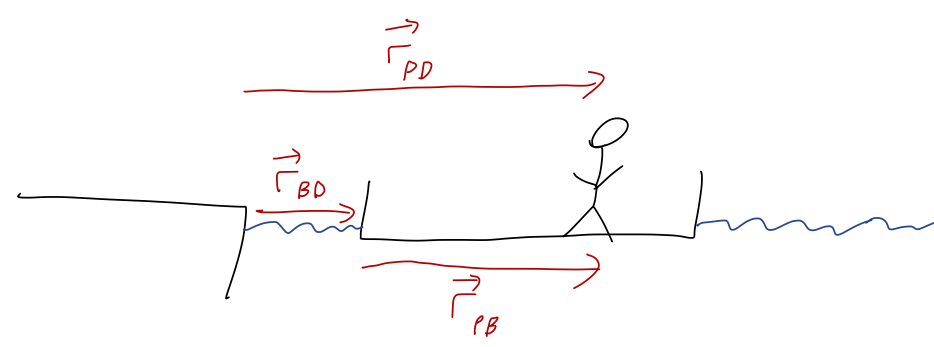
using subscripts for relative position, i.e. \( \vec{r}_{PD} \) is position of the person, relative to the dock. With the coordinate labels as given above, it's clear that there is a relationship between them, namely
\[ \begin{aligned} \vec{r}_{BD} + \vec{r}_{PB} = \vec{r}_{PD}. \end{aligned} \]
Taking time derivatives, the same relation holds for speeds,
\[ \begin{aligned} \vec{v}_{BD} + \vec{v}_{PB} = \vec{v}_{PD}. \end{aligned} \]
Momentum is a different story, because for momentum the mass of each object matters. Since the dock position is fixed, the two momenta we have to keep track of are
\[ \begin{aligned} \vec{p}_{BD} = m_B \vec{v}_{BD} \\ \vec{p}_{PD} = m_P \vec{v}_{PD} \end{aligned} \]
and then \(\vec{P} = \vec{p}_{BD} + \vec{p}_{PD}\) for the total momentum. (Note that we don't need to try to include the person-boat relative motion when defining \( \vec{P} \); we've included all of the moving objects just with these two momentum vectors.)
Given that everything starts at rest, we know that \( \vec{P} = 0 \) at \( t=0 \). Since there are no external forces, momentum conservation thus tells us that \( \vec{P} \) is always zero. This gives us the relation
\[ \begin{aligned} \vec{P} = 0 = m_B \vec{v}_{BD} + m_P \vec{v}_{PD} \\ = m_B \vec{v}_{BD} + m_P (\vec{v}_{BD} + \vec{v}_{PB}) \\ \Rightarrow \vec{v}_{BD} = -\frac{m_P}{m_P + m_B} \vec{v}_{PB}. \end{aligned} \]
In other words, if the person starts walking at speed \( \vec{v}_0 \), the boat moves relative to the dock with speed given in this formula. The minus sign indicates that as we walk away from the dock, the boat moves towards it. We can also plug this in to the relation between the three velocities to find the person's motion relative to the dock:
\[ \begin{aligned} \vec{v}_{PD} = \vec{v}_{BD} + \vec{v}_{PB} = +\frac{m_B}{m_P + m_B} \vec{v}_{PB}. \end{aligned} \]
It's useful to consider the limits of \( m_B \) here. If the boat is very light, say \( m_B \sim m_P \), then it's very easy for our motion to influence the boat's motion; our walking will push the boat towards the dock, and as a result we won't move as quickly away from the dock as we would on dry land. On the other hand, if \( m_B \gg mP \), then \( \vec{v}{BD} \) approaches zero while \(\vec{v}_{PD} \rightarrow \vec{v}_{PB}\). (In other words, for a heavy enough boat, our effect on the boat's motion is imperceptible and it's as if we're just walking on land.)
Just for fun, let's plug in some numbers on a larger-scale example. The largest cruise ship in the world is the Royal Caribbean Symphony of the Seas, with a mass of about 100,000 tons, or \( 9 \times 10^7 \) kg. At maximum capacity, the Symphony can hold 7,718 people. Assuming an average person weighs about 60 kg, what would happen if everyone lined up at one end of the ship and ran to the other end at \( v = 5 \) m/s?
Treating all the people as one mass \( mP = 7718 \times (60\ {\rm kg}) = 4.6 \times 10^5 \) kg moving together, then \( v{PB} \) is 5 m/s, and we can plug in to our formula assuming \( \vec{v}_{BD} = 0 \), i.e. the boat is initially at rest:
\[ \begin{aligned} \vec{v}_{BD} = -\frac{4.6 \times 10^5\ {\rm kg}}{4.6 \times 10^5\ {\rm kg} + 9 \times 10^7\ {\rm kg}} (+5\ {\rm m}/{\rm s}) = 0.025\ {\rm m}/{\rm s} \end{aligned} \]
or 0.06 mph. So I don't think anything noticeable will happen to the ship - it's simply too heavy! (On the other hand, if you've been on a small few-person boat on a lake, you know that your own movements can have a significant effect on how the boat moves.)
External forces and center of mass
Before we move on to apply things, we need to study the effect of external forces a little more. In the presence of an external force, total momentum is not conserved, since
\[ \begin{aligned} \frac{d\vec{P}}{dt} = \vec{F}_{\rm net, ext}. \end{aligned} \]
However, we will find that the way in which the momentum changes due to \( \vec{F}_{\rm net, ext} \) is simple and predictable. So even for problems where external forces are present (and most realistic problems have gravity at least!), we'll be able to split the problem up into the motion due to external force, and then applying momentum conservation for the rest.
Going back to our system of \( N \) point masses, let's now think about their positions \( \vec{r}_1, ..., \vec{r}_N \). Since the momentum of a point mass is
\[ \begin{aligned} \vec{p}_\alpha = m_\alpha \dot{\vec{r}}_\alpha, \end{aligned} \]
we can actually rewrite the total momentum in terms of individual speeds,
\[ \begin{aligned} \vec{P} = \sum_\alpha \vec{p}_\alpha = \sum_\alpha m_\alpha \dot{\vec{r}}_\beta. \end{aligned} \]
Just based on dimensions, if we divide \( \vec{P} \) by a mass scale, we'll get a velocity vector of some sort. Since this is the total momentum, it makes the most sense to divide by the total mass: if
\[ \begin{aligned} M = \sum_\beta m_\beta \end{aligned} \]
then we define the total velocity vector to be
\[ \begin{aligned} \vec{V} = \frac{\vec{P}}{M} = \frac{1}{M} \sum_{\alpha=1}^N m_\alpha \dot{\vec{r}}_\alpha. \end{aligned} \]
Looking at the definition, this is just the time derivative of another vector, which we'll call the center of mass (or "CM") position vector:
\[ \begin{aligned} \vec{V} = \dot{\vec{R}},\ \ \vec{R} = \frac{1}{M} \sum_{\alpha=1}^N m_\alpha \vec{r}_\alpha. \end{aligned} \]
Some references will write this as \(\vec{R}_{CM}\) to be explicit; I'll skip the subscript as long as it's clear from context. The CM vector \( \vec{R} \) gives sort of a weighted average of the positions of all the objects in our system, with weighting proportional to their mass. And now we notice that if we go back to the equation for external net force, we find
\[ \begin{aligned} \frac{d\vec{P}}{dt} = M \ddot{\vec{R}} = \vec{F}_{\rm net, ext}. \end{aligned} \]
So the center of mass position evolves like a point particle with total mass \( M \), following Newton's second law and subject to the net external force acting on the system. This immediately justifies a common approximation used in mechanics, which is that we can treat large, extended objects the same way we treat point particles when applying Newton's laws.
Of course, most everyday objects are pretty complicated, and in fact even a tennis ball is made of an incredible large number of individual tennis-ball particles. For situations where \( N \) would be very large, we can instead replace the sum with an integral. (Think back to your calculus class - this is how integrals are originally defined!)
For the situation where \( N \) is very large, we can replace the discrete set of point masses \( { m_\alpha } \) with a continuous set of infinitesmal masses \( dm \). (Notation aside: curly brackets is math notation for a set, which is a collection of mathematical objects. \( m_\alpha \) denotes one point mass; \( { m_\alpha } \) is the collection of all of them.) Since each tiny speck of mass has its own position, we have to define a function of position \( \vec{r} \) to keep track of them. We define the mass density function \( \rho(\vec{r}) \) through the relationship
\[ \begin{aligned} dm = \rho(\vec{r})\ dV \end{aligned} \]
By inspection \( \rho(r) \) has units of mass per unit volume, \( [M]/[L]^3 \). With this definition, all of the sums over masses become integrals over \( dm \):
\[ \begin{aligned} M = \int dm = \int \rho(\vec{r}) dV \\ \vec{R} = \frac{1}{M} \int \vec{r}\ dm = \frac{1}{M} \int \rho(\vec{r}) \vec{r}\ dV. \end{aligned} \]
and we could write similar formulas for \( \vec{P} \) and \( \vec{V} \), but they're easily obtained by just taking derivatives of \( \vec{R} \).
Don't get confused by the fact that we're integrating over a vector! Since both sides of the equation are vectors, this is really just three separate integrals for each of the components, i.e. in Cartesian components
\[ \begin{aligned} X_{CM} = \frac{1}{M} \int x\ dm,\ \ Y_{CM} = \frac{1}{M} \int y\ dm,\ \ Z_{CM} = \frac{1}{M} \int z\ dm. \end{aligned} \]
The components are almost always found in Cartesian components, even if the integrals themselves are easier to do in cylindrical, spherical, etc. coordinates.
Next time, we'll dig further into the practical details of finding the center of mass for a given physical system.
paigequincluddeas.blogspot.com
Source: https://physicscourses.colorado.edu/phys2210/phys2210_fa20/lecture/lec14-center-of-mass/
0 Response to "Momentum of Fireworks Their Center of Mass Will Continue on the Same Trajectory"
Post a Comment